Základní principy strojového vidění – 7. díl

Prahování

Nejčastěji prahujeme na dvě jasové úrovně — na černou a bílou. Prahování patří mezi základní a nejjednoduší způsoby segmentace obrazu, která má za účel oddělení objektů od pozadí. Kvalita prahování má pro řadu aplikací klíčovou důležitost, např. v případě strojového čtení textů prahování rozhoduje o spolehlivosti procesu a v případech měření v obraze o dosažené přesnosti.

Vlastní prahování je pro jednotlivé pixely snadné a rychlé. Je-li jas pod prahovou hodnotou, přiřadí se pixelu černá barva, pro jas nad prahovou hodnotou se pak přiřadí barva bílá. Celý problém spočívá právě ve volbě té správné prahovací úrovně. Zjištění této hodnoty může být nečekané složitým a výpočetně náročným problémem. Představme si prahování v případě obrazu, kde jas pozadí je velmi nerovnoměrný (což je v případech obrazů snímaných kamerami spíše pravidlem než výjimkou).

Globální prahování

Zde je celý obraz prahován pomocí jediné rozhodovací úrovně. Ta je buď pevně zadána jako konstanta nebo může být zjištěna analýzou obrazu, jako např. jeho střední jas. Metoda je velmi rychlá, ale výše uvedený příklad obrazu je pro ni neřešitelným problémem.

Pro hledání optimálního prahu existuje řada metod, žádná ale dokonale nepokrývá všechny možnosti. Obvykle se využívá toho, že histogram často obsahuje dvě maxima — jedno pro jasy pozadí a jedno pro jasy popředí. Optimální práh pak leží mezi těmito maximy. Často ale nelze jednoznačně rozhodnout o významnosti lokálních maxim histogramu.

Lokální prahování

V tomto případě je pro každý pixel stanovována hodnota lokálního prahu. Lokální práh je tedy funkcí polohy v obraze. Práh tedy již nemůže být zadán jako konstanta a musí být výsledkem analýzy okolí prahovaného bodu. A zde je kámen úrazu, analýza okolí obvykle vyžaduje přístup k alespoň desítkám pixelů vstupního obrazu pro každý jednotlivý prahovaný bod. Toto představuje značnou zátěž pro počítač a zdánlivě jednoduchý krok řetězce zpracování obrazu může limitovat celkový výkon systému.

Výsledek lokálního prahování je přesvědčivý i při nerovnoměrném jasu předlohy.

Víceúrovňové prahování

Výsledkem víceúrovňového prahování již není binární obraz, ale obraz s přesně definovaným počtem jasových úrovní.

Poloprahování

Lze také např. jasům nad prahovací úrovní přiřadit bílou barvu a jasy pod prahovací úrovní ponechat beze změny. Takovému zpracování se říká poloprahovaní nebo také částečné prahování. Tento postup může mít využití např. tam, kde obraz pozoruje a hodnotí člověk.

Detekce hran

Nejen při pozorování obrazu člověkem, ale i pro mnoho algoritmů porozumění obrazu jsou nejdůležitějšími místy obrazu ty, kde se nejvíce mění hodnoty jasu. Procesu, který právě taková místa v obraze automaticky identifikuje, se říká detekce hran. Hrana je v obraze určena jasem pixelu ve vztahu k jasu pixelů v jeho okolí — je určena tím, jak strmě se mění hodnota obrazové funkce. V místě největší strmosti změny dosahuje maxima první derivace funkce a druhá derivace funkce zde prochází nulou. Strmost změny funkce udává její gradient jako vektor, určující směr největšího růstu funkce a strmost tohoto růstu. Pixely na místech velké strmosti růstu obrazové funkce nazýváme hranami.

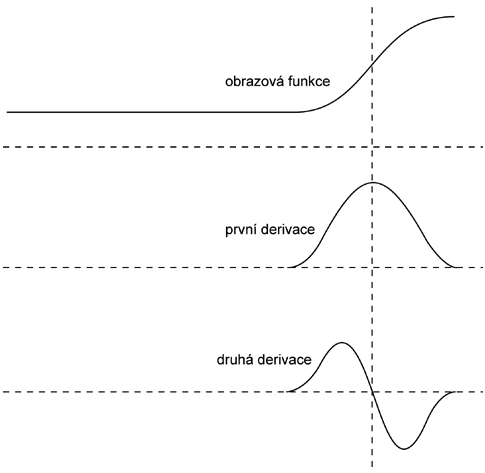
Konvoluční jádra aproximující derivace obrazové funkce

Digitální obraz je maticí diskrétních hodnot jasů. Derivace obrazové funkce můžeme výhodně aproximovat prostřednictvím konvoluce s vhodně zvolenými jádry — tedy můžeme aproximovat derivace pomocí diferencí. Obrazová funkce výsledného obrazu po konvoluci se pak bude více či méně blížit derivaci obrazové funkce vstupního obrazu. První derivace obrazové funkce nabývá svého maxima právě v místech hrany.

Operátory aproximující derivace pomocí diferencí mohou být všesměrové (tedy invariantní vůči rotaci) nebo směrové. V případě všesměrových (např. Laplacián aproximující druhou derivaci) mohou být hrany detekovány konvolucí s jediným jádrem. Jednosměrné operátory, aproximující první derivaci, využívají několik konvolučních jader, odpovídajících příslušné orientaci hrany. Podle výsledků konvoluce je pak vybrán ten operátor, který v daném pixelu nejlépe aproximuje obrazovou funkci. Výběrem jednoho z jader je současně určen i směr vektoru gradientu.

Podstatným problémem detektorů hran je jejich měřítko — velikost konvolučního jádra by měla odpovídat velikosti detailů v obrázku. S měřítkem, a tedy velikostí konvolučního jádra, souvisí i citlivost na šum. V případě malých jader se jejich odezva na šum zvětšuje.

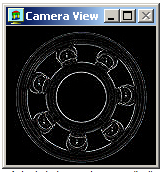
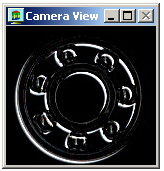
Detekce hran na základě průchodu druhé derivace obrazové funkce nulou

Dobrý detektor hran si obvykle nevystačí s jedinou konvolucí. Je třeba nějak ošetřit i problém měřítka, šumu a nakonec výsledky přiměřeně prahovat (jako příklady řešení mohou sloužit např. Marrův - Hildrethové detektor nebo Cannyho hranový detektor).

Základem detektoru Marrova - Hildrethové je hledání polohy hrany v obraze v místě průchodu druhé derivace obrazové funkce nulou. Hledat polohu hrany v místě průchodu nulou je díky strmosti přechodu mnohem jednoznačnější a spolehlivější než na plochém maximu u první derivace. Důležitá je spolehlivá aproximace druhé derivace. Aproximace druhé derivace konvolucí s patřičným jádrem bývá citlivější na šum (viz. odezva Laplaciánu) než aproximace první derivace. Spolehlivost výpočtu aproximace druhé derivace můžeme zvýšit tak, že na obraz nejdříve použijeme nějaký vyhlazující filtr. Takový filtr může být částečným řešením problémů s měřítkem i se šumem. Na jeho vlastnosti jsou ovšem kladeny přísné požadavky — filtr musí omezovat frekvence, při kterých nemá docházet k průchodu druhé derivace obrazové funkce nulou. Filtr také nesmí posunovat pozici hrany, musí tedy méně reagovat na vzdálenější body od hrany než na body bližší. Používá se proto konvoluce s jádrem, jehož hodnoty se řídí Gaussovým rozdělením. Pixely blíže středu jádra mají při filtraci větší váhu a vliv pixelů vzdálenějších je menší.

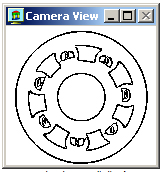
Detekce hran na základě prahování gradientů

Jednodušším a rychlejším postupem může být jednoduchá aproximace první derivace počítající diference každého pixelu od svého okolí. Na základě prahování získaných diferencí jsou pak umísťovány nalezené hrany. Nevýhodou tohoto detektoru je opakované nalézání hran na sousedních pixelech.

Morfologické detekce hran

Morfologické detekce hran pracují na zcela jiných principech, proto patří do této kapitoly jen částečně. Vycházejí totiž z morfologických transformací binárních obrazů, o kterých se budeme zmiňovat v samostatné kapitole. Není zde tedy vyhodnocována strmost změny obrazové funkce, ale vychází se z "pouhého" prahování úrovně jasu. Pro některé případy může být ale právě takový způsob detekce obrysů objektů nejlepším řešením.

Můžeme detekovat vnitřní nebo vnější hrany prahovaných objektů. Princip je velmi jednoduchý. Nejdříve potřebujeme kvalitně prahovaný binární obraz. Algoritmus prahování nám v tomto případě rozhodne o pozici okraje objektů v gradientech jasu na jejich okrajích. Pak v závislosti na tom, chceme-li nalézt vnitřní nebo vnější obrysy objektů provedeme erozi nebo naopak dilataci obrazu. Nakonec vyhodnotíme nonekvivalenci (exkluzivní disjunkce, tj. logická operace XOR ) tohoto upraveného obrazu s obrazem původním a získáme tak přesně jednopixelové souvislé hranové obrysy prahovaných objektů.

Trasování hran

V některých případech, jako je např. identifikace geometrických tvarů, měření velikostí objektů atd., nejsou vyhodnocovány hrany v celém obraze, ale jsou programově trasovány pouze okraje nalezených kontrastních objektů. Principem je opět hledání maximálních diferencí jasů pixelů.

Literatura: Programový systém strojového vidění v prostředí Control Web, Moravské přístroje a.s., www.mii.cz